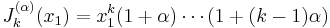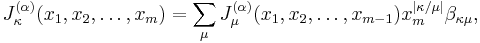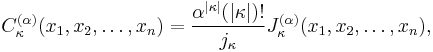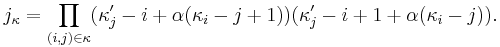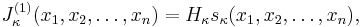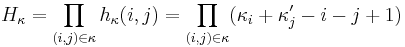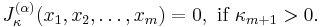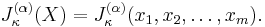Jack function

In mathematics, the Jack function, introduced by Henry Jack, is a homogenous, symmetric polynomial which generalizes the Schur and zonal polynomials, and is in turn generalized by the Heckman–Opdam polynomials and Macdonald polynomials.

1 Definition
2 C normalization
3 Connection with the Schur polynomial
4 Properties
5 Matrix argument
6 References
7 External links

Definition

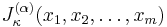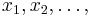The Jack function $J_\kappa^{(\alpha )}(x_1,x_2,\ldots,x_m)$ of integer partition $\kappa$ , parameter $\alpha$ and arguments $x_1,x_2,\ldots,$ can be recursively defined as follows:

For m=1

$J_{k}^{(\alpha )}(x_1)=x_1^k(1%2B\alpha)\cdots (1%2B(k-1)\alpha)$

For m>1

$J_\kappa^{(\alpha )}(x_1,x_2,\ldots,x_m)=\sum_\mu J_\mu^{(\alpha )}(x_1,x_2,\ldots,x_{m-1}) x_m^{|\kappa /\mu|}\beta_{\kappa \mu},$

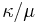where the summation is over all partitions $\mu$ such that the skew partition $\kappa/\mu$ is a horizontal strip, namely

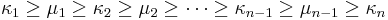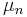$\kappa_1\ge\mu_1\ge\kappa_2\ge\mu_2\ge\cdots\ge\kappa_{n-1}\ge\mu_{n-1}\ge\kappa_n$ ( $\mu_n$ must be zero or otherwise 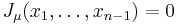$J_\mu(x_1,\ldots,x_{n-1})=0$ ) and

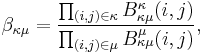
$\beta_{\kappa\mu}=\frac{ \prod_{(i,j)\in \kappa} B_{\kappa\mu}^\kappa(i,j) }{ \prod_{(i,j)\in \mu} B_{\kappa\mu}^\mu(i,j) },$

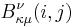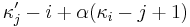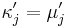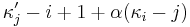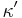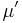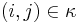where $B_{\kappa\mu}^\nu(i,j)$ equals $\kappa_j'-i%2B\alpha(\kappa_i-j%2B1)$ if $\kappa_j'=\mu_j'$ and $\kappa_j'-i%2B1%2B\alpha(\kappa_i-j)$ otherwise. The expressions $\kappa'$ and $\mu'$ refer to the conjugate partitions of $\kappa$ and $\mu$ , respectively. The notation $(i,j)\in\kappa$ means that the product is taken over all coordinates 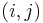$(i,j)$ of boxes in the Young diagram of the partition $\kappa$ .

C normalization

The Jack functions form an orthogonal basis in a space of symmetric polynomials. This orthogonality property is unaffected by normalization. The normalization defined above is typically referred to as the J normalization. The C normalization is defined as

$C_\kappa^{(\alpha)}(x_1,x_2,\ldots,x_n) = \frac{\alpha^{|\kappa|}(|\kappa|)!} {j_\kappa} J_\kappa^{(\alpha)}(x_1,x_2,\ldots,x_n),$

where

$j_\kappa=\prod_{(i,j)\in \kappa} (\kappa_j'-i%2B\alpha(\kappa_i-j%2B1))(\kappa_j'-i%2B1%2B\alpha(\kappa_i-j)).$

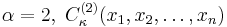For $\alpha=2,\; C_\kappa^{(2)}(x_1,x_2,\ldots,x_n)$ denoted often as just 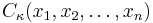$C_\kappa(x_1,x_2,\ldots,x_n)$ is known as the Zonal polynomial.

Connection with the Schur polynomial

When 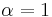$\alpha=1$ the Jack function is a scalar multiple of the Schur polynomial

$J^{(1)}_\kappa(x_1,x_2,\ldots,x_n) = H_\kappa s_\kappa(x_1,x_2,\ldots,x_n),$

where

$H_\kappa=\prod_{(i,j)\in\kappa} h_\kappa(i,j)= \prod_{(i,j)\in\kappa} (\kappa_i%2B\kappa_j'-i-j%2B1)$

is the product of all hook lengths of $\kappa$ .

Properties

If the partition has more parts than the number of variables, then the Jack function is 0:

$J_\kappa^{(\alpha )}(x_1,x_2,\ldots,x_m)=0, \mbox{ if }\kappa_{m%2B1}>0.$

Matrix argument

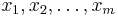In some texts, especially in random matrix theory, authors have found it more convenient to use a matrix argument in the Jack function. The connection is simple. If $X$ is a matrix with eigenvalues $x_1,x_2,\ldots,x_m$ , then

$J_\kappa^{(\alpha )}(X)=J_\kappa^{(\alpha )}(x_1,x_2,\ldots,x_m).$

References

Demmel, James; Koev, Plamen (2006), "Accurate and efficient evaluation of Schur and Jack functions", Mathematics of Computation 75 (253): 223–239, doi:10.1090/S0025-5718-05-01780-1, MR 2176397 .
Jack, Henry (1970–1971), "A class of symmetric polynomials with a parameter", Proceedings of the Royal Society of Edinburgh, Section A. Mathematics 69: 1–18, MR 0289462 .
Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), New York: Oxford University Press, ISBN 0-19-853489-2, MR 1354144
Stanley, Richard P. (1989), "Some combinatorial properties of Jack symmetric functions", Advances in Mathematics 77 (1): 76–115, doi:10.1016/0001-8708(89)90015-7, MR 1014073 .